
Sisu
- Määrake aeg õhus.
- Samm 1
- 2. samm
- 3. samm
- 4. samm
- Määrake maksimaalne kõrgus
- Samm 1
- 2. samm
- 3. samm
- Määrake läbitud horisontaalne kaugus.
- Samm 1
- 2. samm
- 3. samm
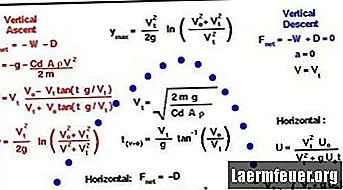
Siin on meetod kuuli trajektoori ja täpsemalt õhus viibimise aja, vahemiku ja selle trajektoori kõrgeima punkti arvutamiseks. Selles näites tehti arvutuse lihtsustamiseks mõned eeldused: tühine õhutakistus, tuule puudumine ja Maa pöörlemise jõustumiseks ebapiisav laskekaugus.
Määrake aeg õhus.
Samm 1
Esiteks tuleb kindlaks määrata vibu kuju. Kui nurk on esialgu allapoole, siis on teadaolevalt juba kõrgeim punkt laskeasend. Isegi ülespoole suunatud nurga all võib sihtmärk olla kõrgeim punkt, olenemata sellest, kas see nurk on madal või piisava kõrgusega (h). Seda saab määrata neljandas etapis, kui määratakse õhuaeg.
2. samm
Kui nurk "?" laskekiirus on mürsu esialgse trajektoori ja horisontaali vahel, nii et algne vertikaalne kiirus on V (i) = V.sen?
3. samm
Õhuaeg leitakse positsiooni h = V.sen?. T - (0,5) g.t ^ 2 võrrandi abil, kus g = 9,8 meetrit / sekundis ^ 2. Kõik muutujad on teada, välja arvatud aeg õhus, t, nii et selle saab lahendada ruutfunktsiooniga: ax ^ 2 + bx + c = 0, seega x = [-b ± √ (b ^ 2-4ac )] / 2a
4. samm
Kui t jaoks on lubatud rohkem kui üks lahendus, kuna h> 0, vastab esimene tulemus väärtusele, kui kõrgus = h tõusuteel, ja teine, kui kõrgus = h laskumisrajal. Kui h <0, siis lubati t ainus tegelik lahendus ja teine on negatiivne.
Määrake maksimaalne kõrgus
Samm 1
Kui? <0, siis on juba teada, et maksimaalne kõrgus on algkõrgus, h = 0.
2. samm
Kui oli rohkem kui üks kord, t, mille jooksul kuul ulatub h, siis väikseim t vastab lennutrajektoorile, kus h on kõrgeim punkt. Suurim t vastab sellele, et täpp jõuab enne h-ni naasmist kõrgemale kõrgusele. Selle kõrguse lahendamiseks kasutage valemit V (t) = V (0) - 9,8t, et leida t väärtus, kui vertikaalne kiirus on null. Teisisõnu, mis ajaks t, V.sen? = 9,8t.?
3. samm
Lahendades t ja ühendades kõrguse valemi, on meil maksimaalne kõrgus: hm = V.sen? - 4,9t ^ 2. Sama lähenemist kasutatakse maksimaalse kõrgusega lahuse puhul, kui lubatud on ainult üks t-lahus.
Määrake läbitud horisontaalne kaugus.
Samm 1
Horisontaalse läbitud kauguse määramiseks ajani, mil kuul jõuab kõrguseni h, arvutage kõigepealt kuuli esialgne horisontaalne kiirus: v (i) = V.cos (?).
2. samm
Asendage aeg t, kui kuul saavutab lõpliku kõrguse A, valemi asendis horisontaalse kiiruse abil: A = V.cosΘ.t. Eeldusel, et paremal küljel puudub õhutakistus ja kiirendustermin.
3. samm
Kui t oli rohkem kui üks kord, kui kõrgus oli h, siis kehtivad kaks tähte "A", kusjuures kõrgeim saavutatud punkt on hm kahest "A" väiksemast. Nüüd on teada horisontaalsed ja vertikaalsed lõppasendid ning kõrgeim saavutatud punkt, mis määravad kuuli trajektoori.